Algorithm
Sort
Merge sort
is a recursive mergesort implementation based on this abstract in-place merge. It is one of the best-known examples of the utility of the divide-and-conquer paradigm for efficient algorithm design.
- Divide array into two halves
- Recursively sort each half
- Merge two halves
| Best | Average | Worst | Space |
|---|---|---|---|
| $$O(nlog(n))$$ | $$O(nlog(n))$$ | $$O(nlog(n))$$ | $$O(n)$$ |
Bucket sort
is a sorting algorithm that works by distributing the elements of an array into a number of buckets.
Bucket sort works as follows:
- Set up an array of initially empty "buckets".
- Scatter : Go over the original array, putting each object in its bucket.
- Sort each non-empty bucket.
- Gather : Visit the buckets in order and put all elements back into the original array.
| Best | Average | Worst | Space |
|---|---|---|---|
| $$O(n+k)$$ | $$O(n+k)$$ | $$O(n^2)$$ | $$O(n)$$ |
Quick sort
Quicksort is a divide and conquer algorithm. Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays.
- Pick an element, called a pivot, from the array.
- Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
- Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.
the worst occurs in following cases.
1) Array is already sorted in same order.
2) Array is already sorted in reverse order.
3) All elements are same (special case of case 1 and 2)
| Best | Average | Worst | Space |
|---|---|---|---|
| $$O(nlog(n))$$ | $$O(nlog(n))$$ | $$O(n^2)$$ | $$O(log(n))$$ |
Selection sort
Selection sort is a sorting algorithm, specifically an in-place comparison sort. It has O(n2) time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort.
- finding the smallest (or largest, depending on sorting order) element in the unsorted sublist
- exchanging (swapping) it with the leftmost unsorted element
- moving the sublist boundaries one element to the right.
| Best | Average | Worst | Space |
|---|---|---|---|
| $$O(n^2)$$ | $$O(n^2)$$ | $$O(n^2)$$ | $$O(1)$$ |
Topological Sorting
directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.
So in the common implementation, we would need two data structure to record how many parents does a node have, and the list of children that node have.
If a question is related to certain order of many nodes, numbers or alphabets, you need to remind that maybe it's a topological sorting problem
Dynamic Programming
Dynamic programming amounts to breaking down an optimization problem into simpler sub-problems, and storing the solution to each sub-problem so that each sub-problem is only solved once.
In bottom-up programming, programmer need to wait the value from the bottom of calculation, then the current recursive can get the actual result . Bottom-up programming is more easier to convert to dynamic programming.
In top-down programming, each recursive would pass the current info to the next recursive, while reaching the bottom of calculation, programmer can get the final result.
Substring
Knuth-Morris-Pratt (KMP)
The problem: given a (short) pattern and a (long) text, both strings, determine whether the pattern appears somewhere in the text.
average : O(m+n)
the implementation is using a “longest suffix-prefix” (LSP) table to precompute pattern
longest suffix-prefix (LSP) table :
public int[] computeLSP(String pattern) {
int[] lsp = new int[pattern.length()];
lsp[0] = 0;
for(int i = 1; i < pattern.length(); i++) {
int j = lsp[i-1];
while(j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = lsp[j - 1];
}
if(pattern.charAt(i) == pattern.charAt(j)) {
j++;
}
lsp[i] = j;
}
return lsp;
}
KMP search :
public int KMPsearch(String txt, String pattern) {
int[] lsp = computeLSP(pattern);
int j = 0;
for(int i = 0; i < txt.length(); i++) {
while(j > 0 && txt.charAt(i) != pattern.charAt(j)) {
j = lsp[j-1];
}
if(txt.charAt(i) == pattern.charAt(j)) {
j++;
if(j == pattern.length()){
return i - (j - 1);
}
}
}
return -1;
Tree
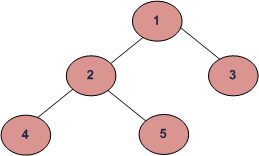
Example Tree
Depth First Traversals:
(a) Inorder (Left, Root, Right) : 4 2 5 1 3
(b) Preorder (Root, Left, Right) : 1 2 4 5 3
(c) Postorder (Left, Right, Root) : 4 5 2 3 1
Breadth First or Level Order Traversal : 1 2 3 4 5
Morris Traversal
traverse the tree without using stack and recursion. The idea of Morris Traversal is based on Threaded Binary Tree.
In this traversal, we first create links to Inorder successor and print the data using these links, and finally revert the changes to restore original tree.
1. Initialize current as root
2. While current is not NULL
If current does not have left child
a) Print current’s data
b) Go to the right, i.e., current = current->right
Else
a) Make current as right child of the rightmost
node in current's left subtree
b) Go to this left child, i.e., current = current->left
Time Complexity : O(n) If we take a closer look, we can notice that every edge of the tree is traversed at-most two times.
Space Complexity : O(1)
Binary Index Tree
Segment Tree
Segment Tree is used for record the minimum or maximum value in a certain range of array, while input is a range query of array
- Partial overlap : if the segment tree's range is partially under the target range, then keep searching the left and right child.
- total overlap: if the segment tree's range is totally under the target range, then return the value of node right away.
- no overlap: if the segment tree's range is not under the target range, then return the a max or min value.
- Segment Tree by array
build tree: O(n) search: O(log(n)) space: O(n)
Example : 307. Range Sum Query - Mutable
class STNode {
int start;
int end;
int sum;
STNode left;
STNode right;
public STNode(int s, int e){
this.start = s;
this.end = e;
}
}
Union Find
dynamic connectivity
- symmetric: If p is connected to q, then q is connected to p.
- transitive: If p is connected to q and q is connected to r, then p is connected to r.
- reflexive: p is connected to p.
Quick Find
using an array to store the union info, all sites in a component must have the same value in id array
Quick Union
id array entry for each site will be the name of another site in the same component, only one value changes while in union operation
Weighted quick-union
Rather than arbitrarily connecting the second tree to the first for union, in the quick-union algorithm, we keep track of the size of each tree and always connect the smaller tree to the larger.
So we need one more extra data structure array to count number of objects in the tree root i
Backtracking
Backtracking is a general algorithm for finding all (or some) solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions, and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot possibly be completed to a valid solution.
Two / Three way partition
Given an array and a range [lowVal, highVal], partition the array around the range such that array is divided in three parts.
1) All elements smaller than lowVal come first.
2) All elements in range lowVal to highVal come next.
3) All elements greater than highVal appear in the end.
The individual elements of three sets can appear in any order.
LFU & LRU
Least Frequently Used (LFU) is a type of cache algorithm used to manage memory within a computer. The standard characteristics of this method involve the system keeping track of the number of times a block is referenced in memory. When the cache is full and requires more room the system will purge the item with the lowest reference frequency.
Least Recently Used (LRU) Discards the least recently used items first.
Random
Reservoir sampling
Reservoir sampling is super useful when there is an endless stream of data and your goal is to grab a small sample with uniform probability.
The math behind is straightforward. Given a sample of size K with N items processed so far, the chance for any item to be selected is K/N. When the next item comes in, current sample has a chance to survive K/N*N/(N+1)=K/(N+1)while the new item has chance K/(N+1) to be selected.
Random r = new Random();
// Iterate from the (k+1)th element to nth element
for (; i < n; i++)
{
// Pick a random index from 0 to i.
int j = r.nextInt(i + 1);
// If the randomly picked index is smaller than k,
// then replace the element present at the index
// with new element from stream
if(j < k)
reservoir[j] = stream[i];
}
Fisher–Yates shuffle
(Knuth shuffle)
The Fisher–Yates shuffle is an algorithm for generating a random permutation of a finite sequence—in plain terms, the algorithm shuffles the sequence.
int[] res = nums.clone();
Random r = new Random();
for(int i = n-1; i >= 0; i--){
int k = r.nextInt(i+1);
swap(res, i, k);
}
Dijkstra's algorithm
for finding the shortest paths between nodes in a graph
we generate a SPT (shortest path tree) with given source as root. We maintain two sets, one set contains vertices included in shortest path tree, other set includes vertices not yet included in shortest path tree. At every step of the algorithm, we find a vertex which is in the other set (set of not yet included) and has a minimum distance from the source.
Time Complexity: The time complexity of the above code/algorithm looks O(V^2) as there are two nested while loops. If we take a closer look, we can observe that the statements in inner loop are executed O(V+E) times (similar to BFS). The inner loop has decreaseKey() operation which takes O(LogV) time. So overall time complexity is O(E+V)*O(LogV) which is O((E+V)*LogV) = O(ELogV)
Space Complexity: O(V)
Notes:
1) The code calculates shortest distance, but doesn’t calculate the path information. We can create a parent array, update the parent array when distance is updated (like prim’s implementation) and use it show the shortest path from source to different vertices.
4) Dijkstra’s algorithm doesn’t work for graphs with negative weight edges. For graphs with negative weight edges, Bellman–Ford algorithm can be used, we will soon be discussing it as a separate post.